Computing Gear Sliding Losses

Introduction

As concerns surrounding the environmental impact of fossil fuels continue to grow, so does the need to produce vehicles with higher overall efficiency. The importance of enhanced vehicles has spurred drivetrain component manufacturers to study every aspect of efficiency loss in their products. The gearbox is a key contributor to the overall drivetrain efficiency. There are several factors that make up inefficiencies in gearboxes. These can be divided into two categories: load-dependent and load-independent. Loaddependent losses (mechanical losses), which include factors such as gear sliding and frictional bearing losses, occur while transmitting a load through the gearbox. Load-independent (spin losses) are due to factors such as bearing, seal, and synchronizer drag, oil churning and gear windage (Ref. 1).

 It is well known that mechanical losses are the predominant sources of lost efficiency. At rated load, empirical studies have shown that gear sliding losses dominate all other sources of mechanical loss — especially at higher speeds (Ref. 2).

Accurately predicting gear sliding losses is critical for increasing gearbox efficiency. The parameters that govern the losses, such as surface finish and sliding velocity, can be effectively optimized for performance and cost if an accurate analytical method is available to predict the effects of these controlling parameters. Significant effort has been devoted to this issue in recent years. Some focused their efforts on the impact that gear geometries played on efficiency, assuming constant coefficient of friction (µ) (Ref. 3).

 Others studied the impact of geometric differences using a more refined approach by utilizing existing experimental formulae to calculate µ (Ref. 4). A benefit of this second approach is that each of the formulae was determined via experimental methods rather than pure theory. On the other hand, the derived equations are only valid within the experimental evaluation parameters, which may limit their application to certain operating conditions, lubricant types and temperatures in practical applications. Finally, some researchers used an elastohydrodynamic lubrication (EHL) approach for improving the prediction of µ (Ref. 5). An extension of past work, this paper documents an effort to enumerate and evaluate the impact of existing formulae of µ on the prediction of gear sliding losses. This is done by establishing the accuracy of each evaluated method against experimental results of various gear sets over a range of operating conditions. Existing Formulae The overall calculation of lost power due to gear sliding as defined in ISO 14179-1 (Ref. 6): (1) P= μ×T×n1×(cos βw) 2 9549×M where P is lost power µ is coefficient of friction T is pinion torque n1 is pinion speed βw is operating helix angle M is mesh mechanical advantage

Formulae Observations

Drozdov and Gavrikov and ISO 14179 predict that µ decreases with increased contact pressure, while Benedict and Kelley and ISO TC60 propose that µ increases with increased contact pressure. Misharin and O’Donoghue and Cameron suggest that load and contact pressure have a negligible effect on µ. The formulae that include surface finish show a proportional relationship with the friction coefficient, while those that incorporate sliding velocity show an inverse relationship with friction coefficient. All equations were empirically formulated: experiments, such as the twin-disk were performed, and a curve was then fit to the results to determine model coefficient values. The disadvantage of this approach is that each equation is only valid within the parameters captured by the experiment, such as lubricant type, temperatures, speed, load, and surface roughness (Ref. 15).

Experimental Procedure

This paper focuses on the realistic application of existing formulae to predict sliding losses using commercially available software. This was accomplished by implementing each of the existing coefficient of friction formulae into Eq. 1 and comparing the results against the measured test stand results. To cover a large spectrum of possible gearbox applications the gearboxes chosen for comparison were a mixture of spur and helical gear sets with various arrangements, the simplest of which was a common FZG type-c spur gear, measured at The Ohio State University Gear Lab (Ref.16). The evaluation then evolved to encapsulate commercially available gearboxes operating with both single- and twin-countershaft layouts. Note that Commercial 2a and 2b represent two power paths within the same gearbox. Each was measured in a controlled test cell environment. The basic parameters of the gearboxes used in this study are shown in Table 2.

Measurements and Lost Power Calculations

The test cells measured input and output power. To compare the analytical results with measured data, some postprocessing of the measurements was required to isolate the experimental sliding losses. The measured spin loss (Input torque = 0) was subtracted from the loaded power loss, leaving gear sliding losses and load-dependent bearing losses. The load-dependent bearing losses were calculated following ISO 14179-1 and then subtracted, leaving only gear sliding losses. This methodology is outlined in equation 2. PSliding=PLoad–PSpin–PBearing (2) where PLoad is loaded measured power loss; PSpin is unloaded measured power loss; PBearing is calculated loaded bearing loss via ISO 14179-1 (Ref.6).

Table 3 shows the normalized results of the testing at 100 N-m over the range of speed tested as an example of the measurements and calculations used to determine the power loss due to gear sliding. The normalized value is calculated as the power loss divided by an arbitrarily selected value.

Finally, the sliding losses were calculated for each of the previously presented empirical formulae corresponding to the measured operating conditions, making a direct comparison between all formulae and measurements possible. For the remainder of this report the term ‘Power Loss’ will refer to sliding losses. Likewise, experimental losses refer to the values as calculated above.

Results and Discussion

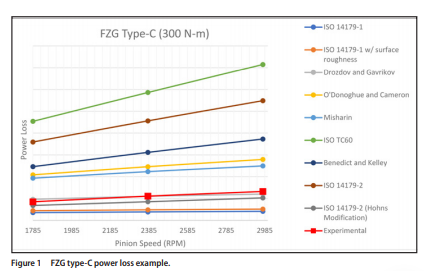
Figure 1 is an example plot of the power loss prediction of each empirical formulae versus pinion speed. Also shown are the experimental data over a range of input speeds and a steady-state torque of 300 N-m. All the predictions follow the same general trend, as input speed increases, the sliding losses also increase. Some, such as ISO TC60 and ISO 14179-2 have a significant vertical offset, indicating over-prediction of losses. Others, such as Drozdov and Gavrikov and ISO 14179-2 (Hohn’s Modification), align more closely with the experimental data. The large number of operating conditions and case studies drove the need for a more concise and numerical assessment of each predictive method. The same dataset shown in Figure 1, along with the remaining operating conditions, were plotted as experimental versus predicted. A linear regression equation was then fit to each for a numerical evaluation of the linear correlation and absolute value relationship between each of the empirical formulae and the experimental data. Figure 2 shows all operating conditions (3 pinion speeds and torque conditions: 9 total), and re-evaluation of ISO TC60 and ISO 14179-2, both of which largely deviated from experimental data in Figure 1. Figure 2 shows that a strong linear relationship exists for each, R 2 of 0.971 and 0.991 respectively, signifying that the predictive variation is not random. A significant offset still exists, 5.89× and 4.37×, indicating that the difference is due to some systematic variation (such as a coefficient) within the empirical formulae, shifting the expected losses well above the actual losses. Others, such as ISO 14179-1 (with and without surface roughness), show an extremely weak linear relationship with the experimental data, suggesting that the variation is more random. Overall, none of these predictive methods are adequate for this dataset. The same procedure was followed to graph the remaining gearboxes. To accurately evaluate each formula over a large spectrum of gearsets and operating conditions, all results were plotted on the same graph. The linear regression equations of each of the formulae are represented in Table 4. Table 4 shows the regression equations of the predicted power loss versus the experimental power loss for each of the 26 data points measured from a variety of gearboxes and operating conditions. All the empirical formulae represent the experimental data reasonably well, with a minimum R2 of 0.69. This suggests that although some may over or under predict, all the methods follow a linear trend that correlates with the experimental results. The best-predicting model for the datasets in this study was Drozdov and Gavrikov, followed by ISO 14179-2 (Hohn’s modification). Both have a strong linear correlation and moderate offset coefficient.